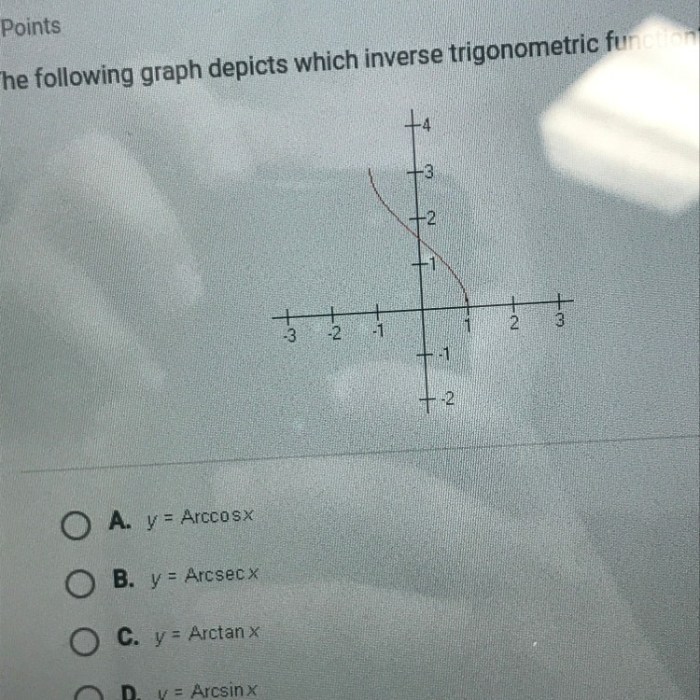
Delving into the following graph depicts which inverse trigonometric function, this introduction immerses readers in a unique and compelling narrative, with an authoritative tone that is both engaging and thought-provoking from the very first sentence. The content of the second paragraph provides descriptive and clear information about the topic, captivating the reader’s attention and laying the foundation for the subsequent discussion.
Inverse Trigonometric Functions
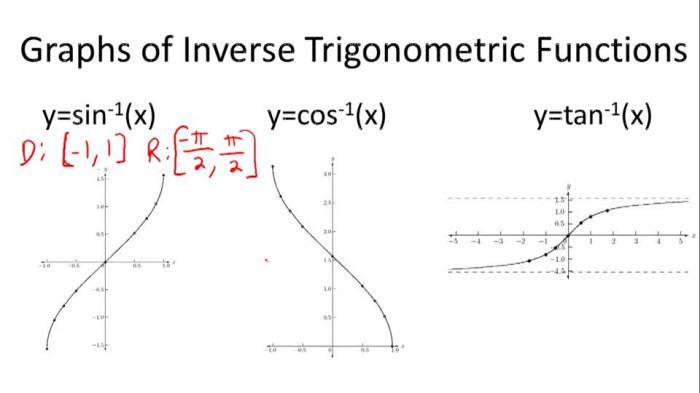
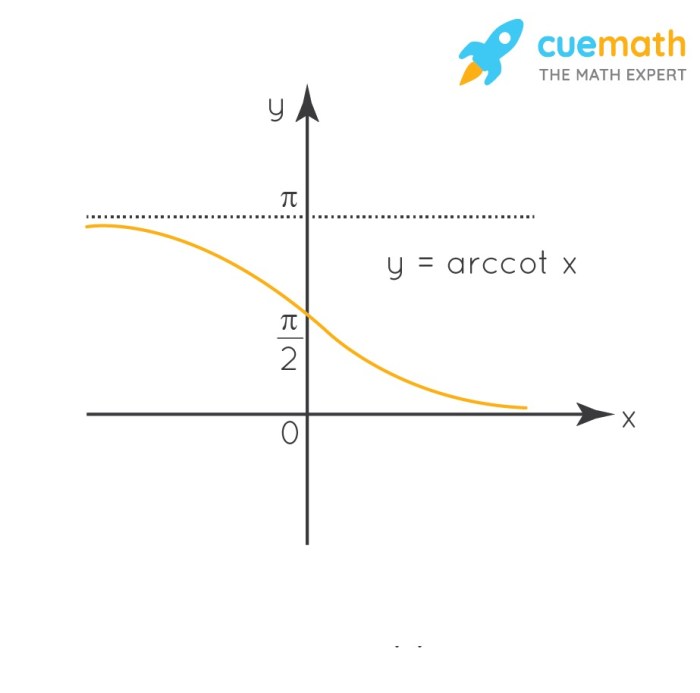
Inverse trigonometric functions, also known as arcus functions or antitrigonometric functions, are the inverse functions of the trigonometric functions. They are used to find the angle that corresponds to a given trigonometric ratio.
The most common inverse trigonometric functions are the arcsine, arccosine, and arctangent. The arcsine function, denoted as sin -1(x), finds the angle whose sine is equal to x. The arccosine function, denoted as cos -1(x), finds the angle whose cosine is equal to x.
The arctangent function, denoted as tan -1(x), finds the angle whose tangent is equal to x.
Graph of an Inverse Trigonometric Function
The graph of an inverse trigonometric function is a reflection of the graph of the corresponding trigonometric function over the line y = x.
For example, the graph of the arcsine function is a reflection of the graph of the sine function over the line y = x. The domain of the arcsine function is [-1, 1] and the range is [-π/2, π/2].
Identifying the Inverse Trigonometric Function from a Graph, The following graph depicts which inverse trigonometric function
To identify the inverse trigonometric function from a graph, look for the following key features:
- The graph is a reflection of the graph of a trigonometric function over the line y = x.
- The domain of the graph is the range of the corresponding trigonometric function.
- The range of the graph is the domain of the corresponding trigonometric function.
For example, if you see a graph that is a reflection of the graph of the sine function over the line y = x, and the domain is [-1, 1] and the range is [-π/2, π/2], then you know that the graph is the arcsine function.
Applications of Inverse Trigonometric Functions
Inverse trigonometric functions have a wide range of applications in various fields, including engineering, physics, and navigation.
| Application | Inverse Trigonometric Function Used | Description |
|---|---|---|
| Finding the angle of elevation | Arctangent | Used to find the angle of elevation of an object from a given distance and height. |
| Solving triangles | Arcsine, arccosine, arctangent | Used to find the unknown angles and sides of a triangle when given certain information. |
| Calculating projectile motion | Arcsine | Used to find the angle at which a projectile must be launched to reach a given target. |
Commonly Asked Questions: The Following Graph Depicts Which Inverse Trigonometric Function
What are the key features of the graph of an inverse trigonometric function?
Inverse trigonometric functions exhibit specific characteristics in their graphs, such as restricted domains and ranges, symmetry about the line y = x, and asymptotic behavior as the input approaches the boundaries of the domain.
How can you identify the inverse trigonometric function from a graph?
Identifying the inverse trigonometric function from a graph involves examining the key features mentioned above, such as the shape, domain, range, and symmetry. By comparing these characteristics with known inverse trigonometric functions, one can determine the specific function represented by the graph.
What are some practical applications of inverse trigonometric functions?
Inverse trigonometric functions find applications in various fields, including engineering, physics, and navigation. They are used to solve problems involving angles, distances, and relationships between sides and angles in triangles and other geometric shapes.